8 Array Formulas
An array formula is a formula that can perform multiple calculations on one or more items in an array. Array formulas were known to be very tricky because they look different from normal formulas and you had to enter these formulas in a different way: with CTRL-SHIFT-ENTER instead of just ENTER. That is no longer the case in Excel 365.
In Excel 365, working with array formulas and their behavior has changed compared to the other Excel versions. Existing formulas that can produce multiple results also behave like array formulas in Excel 365. Some new dynamic array formulas have also been added.
A number of new dynamic array formulas have been added to Excel 365.
By this, the contents of this chapter is largely exclusive to Excel 365.
8.1 What is an Array Formula
A vector is a list of numbers that are either in a row or in a column. You then have a row vector or a column vector respectively. Excel does not use the term vector, but array.
An array in Excel can be:
- A row of values (actually a row vector). This is a 1-dimensional horizontal matrix.
- A column of values (actually a column vector). This is a 1-dimensional vertical matrix.
- A rectangle of rows and columns of values, so an area. This is a 2 dimensional matrix.
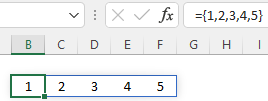
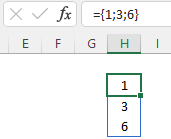
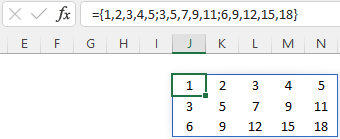
Figure 8.1 shows an example of each.
You can create a matrix with constant values as showed in the three examples, by starting in a cell with the = symbol and then placing a row of values between curly brackets {}. The values must be separated from each other by a special symbol. Which symbols to use as separator symbol depends on the language and regional settings on the computer.
- English language systems
- Comma
,for a new column. - Semicolon
;for a new row.
- Comma
- Dutch language systems
- Backslash `` for a new column.
- Semicolon
;for a new row.
Furthermore, with a 2-dimensional array, you have to take into account:
- List in order of rows.
- All rows must have the same number of columns.
Some examples.
Example 8.1 Row vector
={1,2,3,4,5} returns 1 row with 5 columns.
Example 8.2 Column vector
={1;3;6} returns 3 rows with 1 column.
Example 8.3 2-dimensional array
={1,2,3,4,5;3,5,7,9,11;6,9,12,15,18} returns 3 rows with 5 columns.
For all examples, only the first cell is editable. That is the cell where you entered the array. When you select another cell in the values area, the content in the formula bar is gray, and you cannot change the value.
8.2 Simple Array Formulas
An array formula is a formula that you use to perform calculations on matrices. The result is an array. To use array formulas, you need to consider in advance how many outcomes there are and how these outcomes are arranged (one cell, row, column, table).
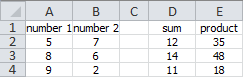
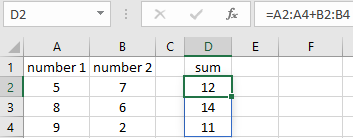
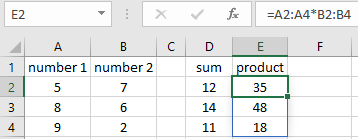
In Figure 8.5, you can see that the sum and product of two numbers are calculated a few times. This can be done with simple formulas. For example, the formula in D2 could be =A2+B2. And the formula in E2 could be =A2*B2. When copying these formulas down the correct formulas are also in D3:E4.
This calculation can also be done with array formulas. It is good practice to learn the behavior of an array formula.
Task 8.1 File: Array1.xlsx
Open the file.
Select cell D2 and enter
=A2:A4+B2:B4and then press ENTER.
The results are in cells D2: D4, and the box around the result shows that it is an array.
More convenient than typing the cell addresses is selecting them with the mouse.
Because the result of the addition consists of a column of three numbers, Excel will automatically flow the result to cells D3:D4. You have to think about this in advance and make sure that these cells are empty, otherwise the error message
#SPILL!will follow.
- Select cell E2 and enter
=A2:A4*B2:B4and then press ENTER.
The results are in cells E2:E4, and the box around the result shows that it is an array.
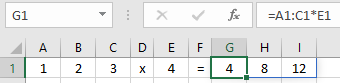
Task 8.2 Multiplication of a row vector with a constant
Figure 8.8 shows how a row of three numbers is multiplied by the number 4. The result consists of a row of three numbers. Make this example yourself.
Formula in G1: =A1:C1*E1
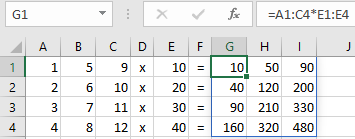
Task 8.3 Multiplication 2-dimensional array with a column vector
Figure 8.9 shows how a 4x3 array is multiplied by a column of numbers. The result is again a 4x3 array.
Make this example yourself. You can use the practicefile Array2.xlsx for this.
Formule in G1 wordt A1:C4*E1:E4
8.3 Calculating one result
This section explains how to use a single array formula in situations that would otherwise require multiple formulas.
You can use an array formula if you need to perform various calculations to get one result. This type of array formula can simplify a worksheet because multiple formulas are replaced by only one array formula.
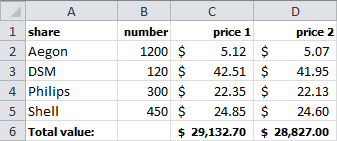
Figure figuur Figure 8.10 shows a stock portfolio with prices. In order to calculate the total value of the shares at a given price you normally calculate the value for each share and then add these values. With an array formula, this calculation can be done without calculating the intermediate results.
Task 8.4 File: Array3.xlsx
Open the file.
Select cell C6 and enter formula
=SUM(B2:B5*C2:C5).Repeat this action for cell D6, the entered formula is
=SUM(B2:B5*D2:D5).
Question
You can also make the formula in C6 suitable for copying to D6. What do you have to change in the formula for that?
By making the first column in the formula in C6 absolute, so =SUM($B$2:$B$5*C2:C5).
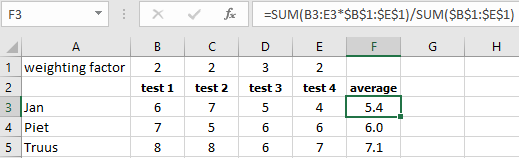
Task 8.5 File: Array4.xlsx
In this exercise, the weighted average of four tests must be calculated for each student using a matrix formula. Start with a formula for Jan and make this formula suitable for copying down.
You get a weighted average for Jan by multiplying each test grade of Jan by the weighting factor for that test and then dividing the sum of these four results by the sum of the four test factors.
To make the formula suitable for copying, you have to think about which cell addresses should not be changed during copying. You have to make those cell addresses absolutely.
Formula F3: =SUM(B3:E3*$B$1:$E$1)/SOM($B$1:$E$1)
Then copy formula to F4 and F5.
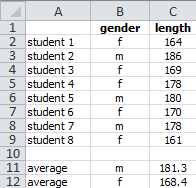
Task 8.6 File: Array5.xlsx
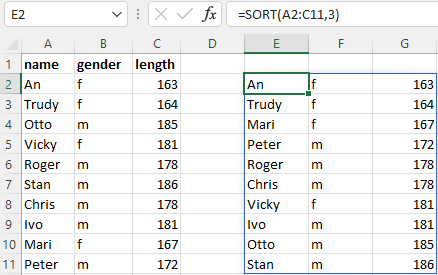
Figure 8.12)shows the gender and height (cm) of a number of students. The average height for male and female students is calculated in the cells C11 and C12.
The array formula is a bit trickier here because you only need to select the lengths for either male or female. This is possible with the IF function.
Open the file.
Select cell C11 and enter formula
=AVERAGE(IF(B2:B9="m",C2:C9)).Now create a formula for cell C12 by adjusting the formula for the female students.
Formula C12: =AVERAGE(IF(B2:B9="f",C2:C9)).
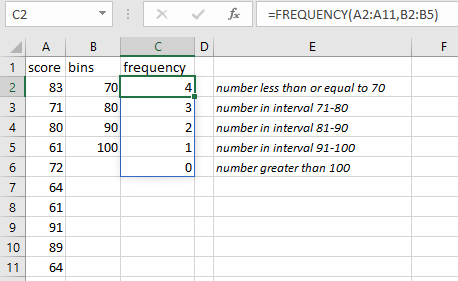
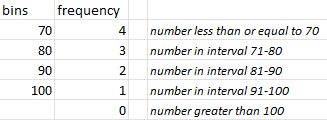
8.4 Frequency distribution
With function FREQUENCY you can create a frequency distribution.
Syntax: FREQUENCY(data_array,bins_array).
The first argument is an array with the values. The second argument is an array with the intervals into which you want to group the values. The result is an array with the frequencies.
8.5 Dynamic array formulas
An array formula entered in one cell on the worksheet can give results in multiple cells on the worksheet. This behavior is called spilling, and the results appear in a spill range. Which cells and how many depends on the result of the formula. If the source content of the formula changes, the results are dynamically updated, and the spill range may grow or shrink. You get an #SPILL! Error when the spilling is blocked by other data in the cells.
To create a reference to a spill range, put a hash symbol # after the address of the first cell of the spill range. For example, if the spill range is J2:N4, you refer to it with=J2#. When on a later moment, the size of the spill range changes, the result of the formula also changes.
When you are using arrays in formulas, it is very useful to provide them with a name. This can be done the same way you are assigning a name to a cell.
To support the behavior of dynamic arrays, a number of new functions have been released: RANDARRAY, FILTER, SEQUENCE, SORT, SORTBY, UNIQUE, XMATCH and XLOOKUP.
8.5.1 RANDARRAY
Returns an array with random numbers. All arguments are optional.
Syntax
RANDARRAY([rows],[columns],[min],[max],[integer])
rows: the number of rows in the returned array (default=1)columns: the number of columns in the returned array (default=1)min: the minimum number you would like returned (default=0)max: the maximum number you would like returned (default=1)integer: TRUE for returning integers, FALSE for returning decimals (default = FALSE)
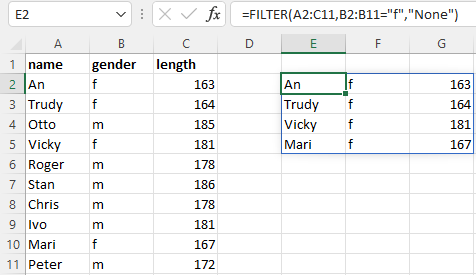
8.5.2 FILTER
Returns the filtered values from an array/range.
Syntax
FILTER(array,include,[if_empty])
array: the range or array to filter.include: an array of booleans where TRUE represents a row or column to retain.if_empty: returned value if no items are retained.
Example 8.5 File: Dynarray.xlsx
Extract the rows with gender female.
Replace in the formula “f” with “m” or “z”.
You can also add multiple criteria. To filter for women less than 170 change the formula in =FILTER(A32:C41,(B32:B41="f")*(C32:C41<170),"None")
8.5.3 SEQUENCE
Returns a sequence of numbers according to a pattern.
Syntax
SEQUENCE(rows,[columns],[start],[step])
rows: the number of rows to return.columns: the number of columns to return (default=1)start: the first number in the sequence (default=1)step: the amount to increment each subsequent value in the sequence (default=1)
8.5.4 SORT
Sorts the column values from a range/array.
Syntax
SORT(array,[sort_index],[sort_order],[by_col])
array: the array to sort.sort_index: a number indicating the row or column to sort by (default=1)sort_order: 1= the sort order, 1=ascending, -1=descending (default=1)by_col: logical value for the sort direction, TRUE=sort columns, FALSE=sort rows (default=FALSE)
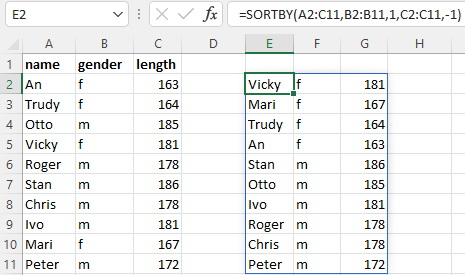
8.5.5 SORTBY
Sorts the values from a range/array based on other values.
Syntax
SORTBY(array,by_array1,[sort_order], ...)
- array: the array to sort.
- by_array1: the array to sort on
- sort_order: 1= the sort order, 1=ascending, -1=descending (default=1)
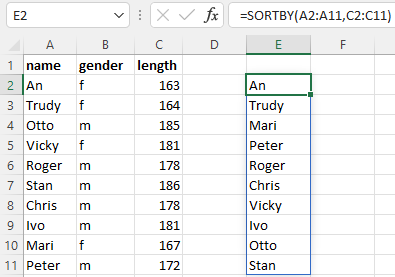
Example 8.8 File: Dynarray.xlsx
Sort names based on length.
=SORTBY(A2:A11,C2:C11)
As you can see, the series on which the sort is based does not have to appear in the output.
Another use of this function is when sorting by two columns.
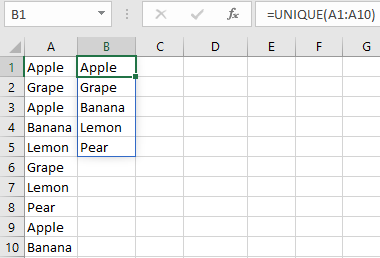
8.5.6 UNIQUE
Returns an array with unique values from an array.
Syntax
UNIQUE(array,[by_col],[exactly_once])
array: the array from which to return unique rows or columns.by_col: TRUE=return unique columns, FALSE= return unique rows (default=FALSE)exactly_once: TRUE=returns unique values that occur exactly once, FALSE=returns all distinct rows or columns (default = FALSE)
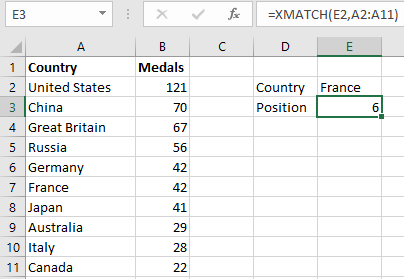
8.5.7 XMATCH
The function performs a search and returns a position in vertical or horizontal ranges. It is a modern and more extensive successor of the function MATCH.
XMATCH supports approximate and exact matches, reverse search, and wildcards (*?) for partial matches. The data lookup can start from the first value or from the last value (reverse search). In addition, binary searches can also be performed.
This function is usually used in conjunction with other functions. Much more useful is the XLOOKUP function.
Syntax
XMATCH(lookup_value,lookup_array,[match_mode],[search_mode])
lookup_value: the value to search forlookup_array: the array to searchmatch_mode: specify how to match, 0=exact match, -1=exact match or the next smaller item, 1=exact match or the next larger item, 2=wildcard match (default=0)search_mode: specify how to search, 1=start search from the first item, -1=from the last item, 2=binary ascending, -2=binary descending
8.5.8 XLOOKUP
This function is a modern and more comprehensive replacement for older functions like VLOOKUP, HLOOKUP and SEARCH. This new function supports approximate and exact matches, wildcards (*?) for partial matches, and search capabilities in vertical and horizontal ranges.
Syntax
XLOOKUP(lookup_value, lookup_array, return_array, [if_not_found], [match_mode], [search_mode])
lookup_value: the value to search forlookup_array: the array to searchreturn_array: the array to returnif_not_found: the value to return if no match is foundmatch_mode: specify how to match, 0=exact match, -1=exact match or the next smaller item, 1=exact match or the next larger item, 2=wildcard match (default=0)search_mode: specify how to search, 1=start search from the first item (default), -1=from the last item, 2=binary ascending, -2=binary descending
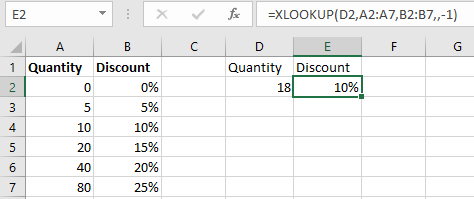
Example 8.12 =XLOOKUP(D2,A2:A7,B2:B7,,-1)
A discount table containing the discount percentages from a certain quantity.
Pay close attention to the arguments in this formula.
lookup_value: D2lookup_array: A2:A7return_array: B2:B7if_not_found: is not specified, hence a comma immediately follows.match_mode: -1search_mode: is not specified, the default value will be used.
8.6 Tables and array formulas
In most cases, array formulas are used to perform actions on a list of data, often in multiple columns. Then it has many advantages to turn that data list into a real Excel table. In the array formulas you can then use the table and column name for the references. And the references remain healthy when rows are added or removed.
When referring to a column name in an Excel table, put the column name in square brackets immediately after the table name: table_name[column_name].
Task 8.8 File: Personnel.xlsx
Open the file.
Convert the data range to a table with tab Insert > Table and specify tblPersonnel as the name of the table.
Save the file with name
Personneltable.xlsxso that the original file is not modified.In a cell outside the data area, e.g. in cell K4, enter the following formula
=UNIQUE(tblPersonnel[Department]).
You will now get a list with the names of the departments. To make an alphabetically sorted list of these, you have to include this formula within the function SORT.
- Change the entered formula to
=SORT(UNIQUE(tblPersonnel[Department])).
You will now get a sorted list with the names of the departments.
Similarly, create a sorted list of division names.
8.7 Returning multiple values
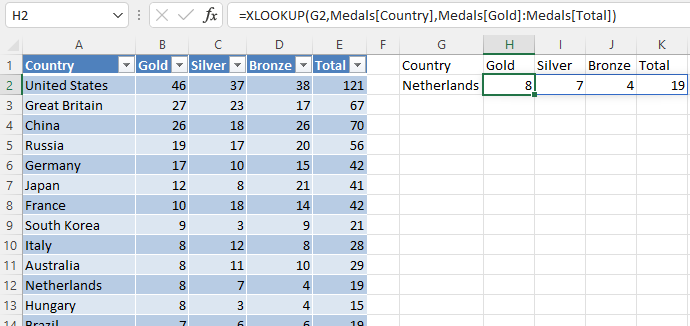
XLOOKUP can return more than one value for the same match. In this task, four values are returned with one formula.
Task 8.9 File: olympic2016.xlsx
Open the file.
Convert the data range to a table with tab Insert > Table and specify Medals as table name.
Add a Total column to the table containing a formula for the total number of medals. This is done as follows:
Enter the text
Totalin cell E1 and press ENTER. A new column is now automatically created.Select cell E2 and type
=SUM(]{.userinput}, then select the cells B2:D2, type [)and press ENTER.
The values now appear in the Total column. Note further that Excel has changed the formula in cell E2 in =SOM(Medals[@[Gold]:[Bronze]]).
Copy the texts in A1:E1 to G1:K1.
Enter the text
Netherlandsin cell G2.Select H2 and enter
=XLOOKUP(G2,Medals[Country],Medals[Gold]:Medals[Total]).
The result will look like this:
8.8 Two way search
XLOOKUP can also be used to search in two directions. This can be done by including (nesting) an XLOOKUP function within another XLOOKUP function.
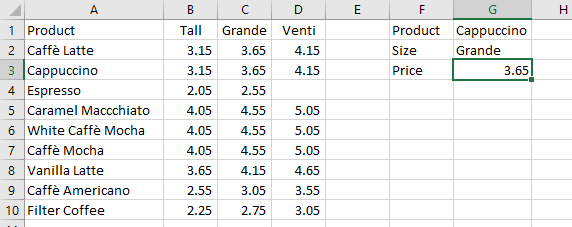
Figure 8.24 shows a number of Starbucks coffee prices. In cell G3, the price must appear based on the search criteria in G1 and G2.
Task 8.10 File: Tidy001.xlsx
Open the file.
Enter the data in F1:F3 and G1:G2.
Enter in G3 the formula
=XLOOKUP(G2,B1:D1,XLOOKUP(G1,A2:A10,B2:D10)).
The inner
XLOOKUPlooks up the coffee type in the product column and returns a row with the three prices.The outer
XLOOKUPfinds the correct size and returns the corresponding price.
8.9 Mathematical array functions
Especially in linear algebra, many arithmetic operations are performed with arrays. Excel offers support for this with a few specific functions. The use of these functions is beyond the scope of this textbook.
- MUNIT
- Identity matrix.
- Returns the identity matrix for the specified dimension. Mostly used in combination with other matrix functions, such as MMULT.
- MMULT
- Matrix product.
- Returns the matrix product of two arrays.
- MINVERSE
- Inverse matrix.
- Returns the inverse matrix. Generally used for solving systems of mathematical equations with several variables. The product of a matrix and its inverse is the identity matrix.
- MDETERM
- Determinant.
- Returns the determinant of a matrix. Generally used for solving systems of mathematical equations with several variables.
8.10 Exercises
Exercise 8.1 Array addition (matr001)
Enter the following summation using array formulas.

Exercise 8.2 Failures per district (matr002)
The public utility of a city keeps a list for recording per district the reported failures to gas, water, and electricity. You can see this list in the following figure. The management of the company would like an overview of the total number of failures per district as calculated under the resume. The easiest way to do this is by using array formulas.
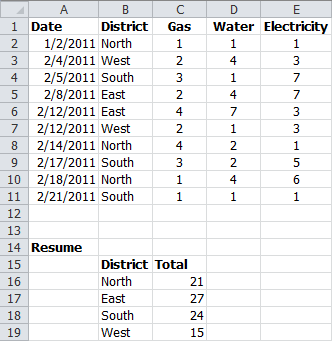
File: Matr002.xlsx
Enter the array formulas in the cells C16, C17, C18 en C19 to calculate the total number of failures per district.
- The formula {(B2:B11)=B16} provides a matrix column of 10 rows. If the value in a cell from the range B2:B11 is equal to the value in cell B16 (= North) then the value in the array is TRUE (=1) otherwise FALSE (=0).
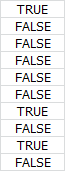
- By multiplying the column array with the array {C2:E11} you get a new array of 10 rows and three columns. The cells in the rows which are multiplied with FALSE get all the value zero. The cells which are multiplied with TRUE keep their original values:
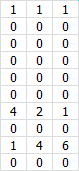
- Calculating the sum of all these values gives you the total number of failures for the district North.
Exercise 8.3 Random integers (matr003)
With function RANDARRAY you can generate random numbers. To experiment with this and study the behavior of the dynamic array formulas, create a new file with the following data:
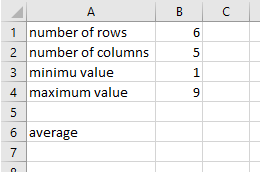
- In cell B7, enter the formula to generate random integers, referring to cells in B1 through B4 for the first four arguments.
- Enter a formula in cell B6 to calculate the average of the generated numbers. Use a reference to the spill range.
- Experiment with different values in cells B1 through B4. Note that the maximum value cannot be less than the minimum value.
Exercise 8.4 Random dates and times (matr004)
Dates and times are stored internally in Excel as a number. For example, 2020-06-30 18:00:00 will be stored internally as 44012.75.The part before the comma is the date and the part after the comma is the time.Since you can generate random numbers with the RANDARRAY function, you can also generate dates and times with it. The figure below shows an example.
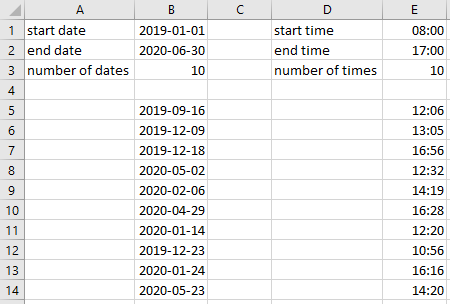
- In a new worksheet, enter the data for the first three rows and apply correct formatting.
- Enter a formula in cell B5 to generate the dates and in cell E5 a formula to generate the times. Use the data in the first three rows as arguments. In the spill range you have to apply the correct formatting for dates or times because that does not happen automatically.
- Experiment with different values in the first three rows. Note that the maximum value cannot be less than the minimum value.
Exercise 8.5 Sorting columns (matr005)
The figure below shows the population size of the Benelux countries for the years 2000, 2005, 2010 and 2015. If you want this data for the years in reverse order, you can easily do this with the dynamic array formula SORT, which also allows you to sort columns.
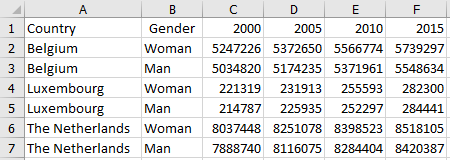
File: Benelux-Population.xlsx
Open the file and copy the data in columns A and B respectively to H and I. Now enter the formula SORT in cell J1 so that the data for the years appears in descending order. The result should look like this.
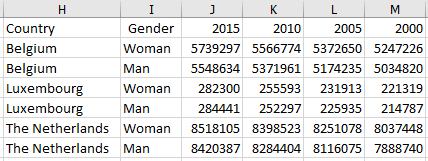
If you want to keep the file, save it under the name matr005.xlsx, then the original file is not changed.
Exercise 8.6 Sequence of Roman numbers (matr006)
In a new worksheet, create an array with the numbers 1 to 100 as in the following figure.
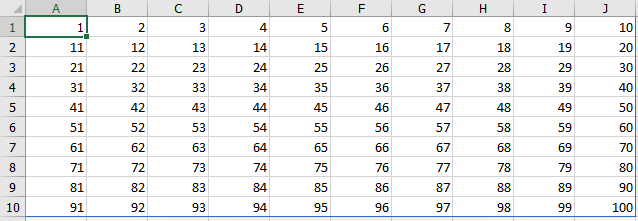
Then change the formula so that you get Roman numbers.
Function ROMAN converts Arabic numbers to Roman numbers, as text.
If you want to keep the file, save it under the name matr006.xlsx.